Cubic Spline (cspline) Object

 Type: Object
 Data: Two data vectors that define 1D function points
 Inputs: Name of first data column (e.g. x)
 Outputs: Name of second data column (e.g. y)
 Description: Cubic spline for nonlinear function approximation

A cubic spline is a nonlinear function constructed of multiple third-order polynomials. These polynomials pass through a set of control points and have continuous first and second derivatives everywhere. The second derivative is set to zero at the left and right endpoints, to provide a boundary condition to complete the system of equations. There is poor extrapolation when function retrievals are requested outside of the data points. The input should be constrained or else additional data points added to avoid extrapolation.

Example Usage

Find the maximum of a function defined by 8 points that approximate the true function.

$y(x) = \frac{1}{1+25 x^2}$

The function is evaluated at the points x_data = [-1.0 -0.8 -0.5 -0.25 0.0 0.1 0.2 0.5]. Evaluating at additional points shows the cubic spline interpolation function. The maximum of the original function is at x=0 with a result y=1. Because the cubic spline has only 8 points, there is some approximation error and the optimal solution of the cubic spline is slightly to the left of the true solution.

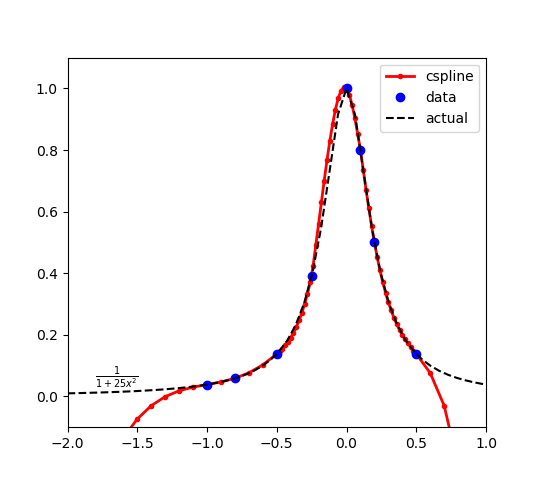
The cubic spline intersects the points to create the function approximations in the range of x between -1.0 and 0.5. There is extrapolation error outside of this range, as expected. Bounds on x should be added or additional cubic spline sample points should be added to avoid problems with optimizer performance in the extrapolation region.

APM Python Example

Use the following x and y data to construct a cubic spline.

  x_data         ,  y_data
  -1.0000000e+00 ,  3.8461538e-02
  -8.0000000e-01 ,  5.8823529e-02
  -5.0000000e-01 ,  1.3793103e-01
  -2.5000000e-01 ,  3.9024390e-01
   0.0000000e+00 ,  1.0000000e+00
   1.0000000e-01 ,  8.0000000e-01
   2.0000000e-01 ,  5.0000000e-01
   5.0000000e-01 ,  1.3793103e-01

Find the maximum of the interpolated function.

GEKKO Python Example

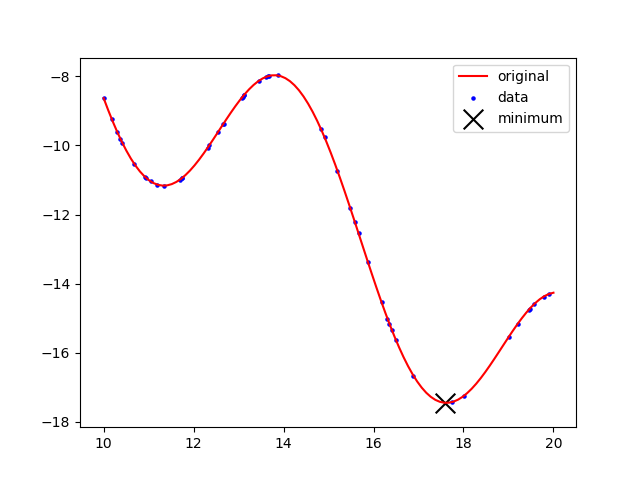
Sample the function $3\sin(x)-(x-3)$ at 50 random points between 5 and 15. Use the randomly sampled points to construct a cubic spline and find the minimum of that function.

See also B-Spline Object for 2D surface function approximations from data

APMonitor