Integer Linear Programming
Integer Linear Programming (ILP) is a type of optimization problem where the variables are integer values and the objective function and equations are linear.
$$ \begin{align} & \text{maximize} && \mathbf{c}^\mathrm{T} \mathbf{x}\\ & \text{subject to} && A \mathbf{x} \le \mathbf{b} \\ & && \mathbf{x} \ge \mathbf{0} \\ &&& \mathbf{x} \in \mathbb{Z}^n \end{align} $$
A Mixed-Integer Linear Programming (MILP) problem has continuous and integer variables. Mixed-Integer Nonlinear Programming (MINLP) also includes nonlinear equations and requires specialized MINLP solvers such as APOPT. MINLP solvers can also solve MILP or ILP problems although other solvers such as CPLEX, Gurobi, or FICO Xpress are specialized commercial solvers for MILP. APMonitor and GEKKO solve MINLP problems. The following integer linear programming (ILP) problem has a two potential maximum values at (1,2) and (2,2).
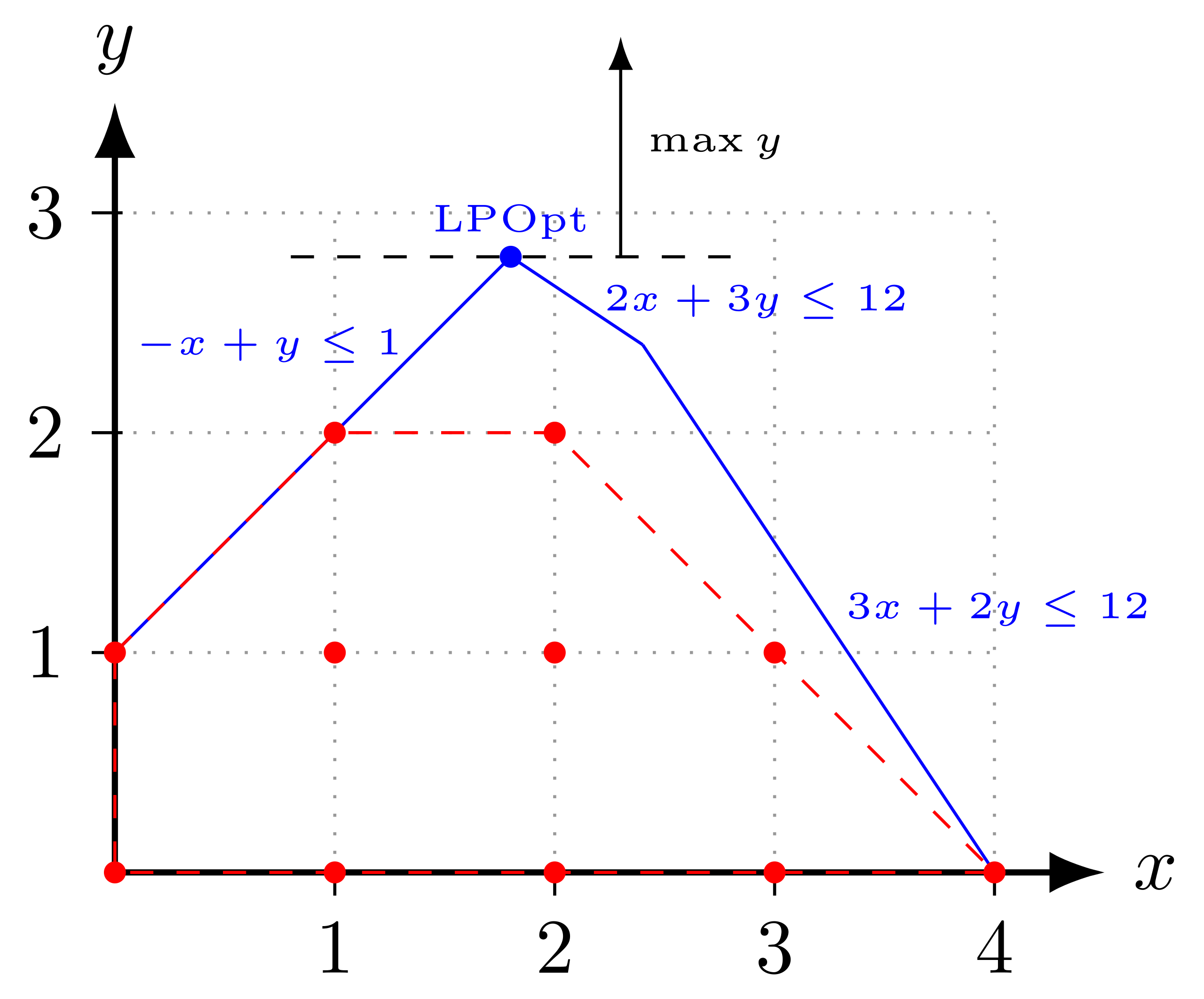 | $$\begin{align} \max & \text{ } y \\ -x +y & \leq 1 \\ 3x +2y & \leq 12 \\ 2x +3y & \leq 12 \\ x,y & \ge 0 \\ x,y & \in \mathbb{Z} \end{align}$$ |
APMonitor Model File
Integer variables are declared in APMonitor with the prefix int. The problem is solved with MATLAB, Julia, Python or through the APMonitor Online Interface.
Variables
int_x >= 0
int_y >= 0
End Variables
Intermediates
x = int_x
y = int_y
End Intermediates
Equations
maximize y
-x+y<=1
3*x+2*y<=12
2*x+3*y<=12
End Equations
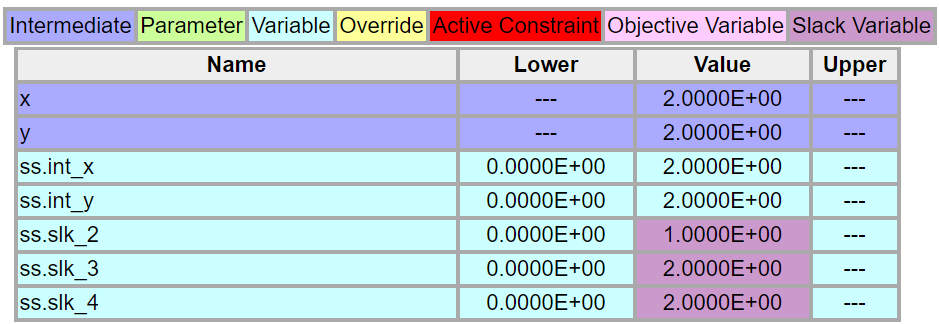
Python Gekko
Gekko is a Python API to APMonitor. The same ILP problem is solved with Gekko.
m = GEKKO()
x,y = m.Array(m.Var,2,integer=True,lb=0)
m.Maximize(y)
m.Equations([-x+y<=1,
3*x+2*y<=12,
2*x+3*y<=12])
m.options.SOLVER = 1
m.solve()
print('Objective: ', -m.options.OBJFCNVAL)
print('x: ', x.value[0])
print('y: ', y.value[0])
--------------------------------------------------- Solver : APOPT (v1.0) Solution time : 0.0852 sec Objective : -2. Successful solution --------------------------------------------------- Objective: 2.0 x: 2.0 y: 2.0
Nonlinear programming solvers (such as IPOPT) may not return an integer solution because they are designed for continuous variables. Mixed Integer Nonlinear Programming solvers (such as APOPT) are equipped to solve for binary or integer variables. It is selected with m.options.SOLVER=1. Select the appropriate solver option to either find an initial solution without integer variables or an integer solution. It is sometimes desirable to find a non-integer solution first because of the often significant reduction in computation time without the integer variables.
Solution in Matrix Form
Another representation is matrix form. Gekko function qobj defines a linear or quadratic objective and axb defines the `Ax\leb` constraint.
m = GEKKO(remote=False)
c = [0,1]
A = [[-1,1],[3,2],[2,3]]
b = [1,12,12]
z = m.Array(m.Var,2,integer=True,lb=0)
m.qobj(c,x=z,otype='max')
m.axb(A,b,x=z,etype='<=')
m.options.SOLVER = 1
m.solve()
print('Objective: ', -m.options.OBJFCNVAL)
print('x: ', z[0].value[0])
print('y: ', z[1].value[0])
Solution in Sparse Matrix Form
For large-scale problems, it is more efficient to solve the problem in sparse matrix form. The matrix arguments are passed to Gekko in coordinate (COO) list form. COO list form is [row indices],[values] for a vector and [row indices],[column indices],[values] for a matrix.
m = GEKKO(remote=False)
c = [[2],[1]]
A = [[1,1,2,2,3,3],[1,2,1,2,1,2],[-1,1,3,2,2,3]]
b = [[1,2,3],[1,12,12]]
z = m.Array(m.Var,2,integer=True,lb=0)
m.qobj(c,x=z,otype='max',sparse=True)
m.axb(A,b,x=z,etype='<=',sparse=True)
m.options.SOLVER = 1
m.solve()
print('Objective: ', -m.options.OBJFCNVAL)
print('x: ', z[0].value[0])
print('y: ', z[1].value[0])
Additional Resources