Stirred Reactor
Reactor
The continuously stirred tank reactor is a popular model for benchmarking. It is a simple A to B reaction and has exothermic reaction instability with a prolonged cooling jacket temperature above 305 K.
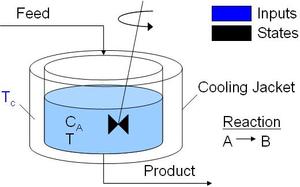
See also Van de Vusse Reactor
CSTR Simulation with Python
! APMonitor Modeling Language
! https://www.apmonitor.com
! CSTR model from
! Michael A. Henson and Dale E. Seborg. Nonlinear
! Process Control. Prentice Hall PTR, Upper
! Saddle River, New Jersey, 1997.
! Description:
! Continuously Stirred Tank Reactor with energy
! balance and reaction A->B.
! The temperature of the cooling
! jacket is the control.
Model cstr
Parameters
! Manipulated Variables
Tc = 270 ! Temperature of cooling jacket (K)
! Parameters
q = 100 ! Volumetric Flowrate (m^3/sec)
V = 100 ! Volume of CSTR (m^3)
rho = 1000 ! Density of A-B Mixture (kg/m^3)
Cp = .239 ! Heat capacity of A-B Mixture (J/kg-K)
mdelH = 5e4 ! Heat of reaction for A->B (J/mol)
! E - Activation energy in the
! Arrhenius Equation (J/mol)
! R - Universal Gas Constant
! = 8.31451 J/mol-K
! EoverR = E/R
EoverR = 8750
k0 = 7.2e10 ! Pre-exponential factor (1/sec)
! U - Overall Heat Transfer
! Coefficient (W/m^2-K)
! A - Area - this value is specific
! for the U calculation (m^2)
! UA = U * A
UA = 5e4
Caf = 1 ! Feed Concentration (mol/m^3)
Tf = 350 ! Feed Temperature (K)
End Parameters
Variables
! Differential States
Ca = 0.9 ! Concentration of A in CSTR (mol/m^3)
T = 305 ! Temperature in CSTR (K)
End Variables
Equations
! note: the $ denotes time differential
! (e.g. $x is dx/dt)
! mole balance for species A
V * $Ca = q*(Caf-Ca) - k0*V*exp(-EoverR/T)*Ca
! energy balance
rho*Cp*V * $T = q*rho*Cp*(Tf - T) + V*mdelH*k0*exp(-EoverR/T)*Ca + UA*(Tc-T)
End Equations
End Model