High Index DAE Solution
Solve high index Differential and Algebraic Equations (DAEs) without rearrangement or differentiation. A common method for high index DAEs is to use Pantelides algorithm to reduce the index order. The index of a DAE is the number of times the equations must be differentiated to return to index-0 (ODE) form. Most ODE and DAE solvers have several challenges:
- Consistent initial condition is required
- Required index-1 or index-2 (Hessenberg form)
- Numerical drift with repeated differentiation
APMonitor and Gekko overcome these challenges by solving high index DAEs without differentiation with orthogonal collocation on finite elements and efficient sparse solvers.
Index-0 to Index-3 Pendulum Example
A pendulum is used to investigate the effect of Differential and Algebraic (DAE) index with index-0 to index-3 DAE forms of the same model. The pendulum weight is located on the end of a massless cord suspended from a pivot, without friction. When given an initial push, it swings back and forth at a constant amplitude. Real pendulums are subject to friction and air drag, so the amplitude of the swing declines. The pendulum equations of motion calculate x-axis and y-axis positions as x and y and velocities as v and w, respectively. Additional parameters include m as the mass of pendulum, g as a gravitational constant, and s as the length of pendulum. The variable `\lambda` is a Lagrange multiplier.
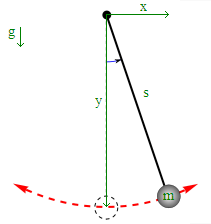
Index-0 DAE
$$\frac{d\lambda}{dt} = \frac{-4 \lambda \left( x \, v + y \, w \right) }{x^2+y^2}$$
Index-1 DAE
$$m \left( v^2 + w^2 - g \, y \right) - 2 \lambda \left( x^2 + y^2 \right) = 0$$
Index-2 DAE
$$x \, v + y \, w = 0$$
Index-3 DAE
$$x^2 + y^2 = s^2$$
The models are mathematically equivalent but are of different index order. The most natural form is an index-3 DAE equation form, posed in terms of absolute position. The index is the number of times the equations must be differentiated to achieve an ordinary differential equation (ODE) form. This differentiation can cause numerical drift as seen in the
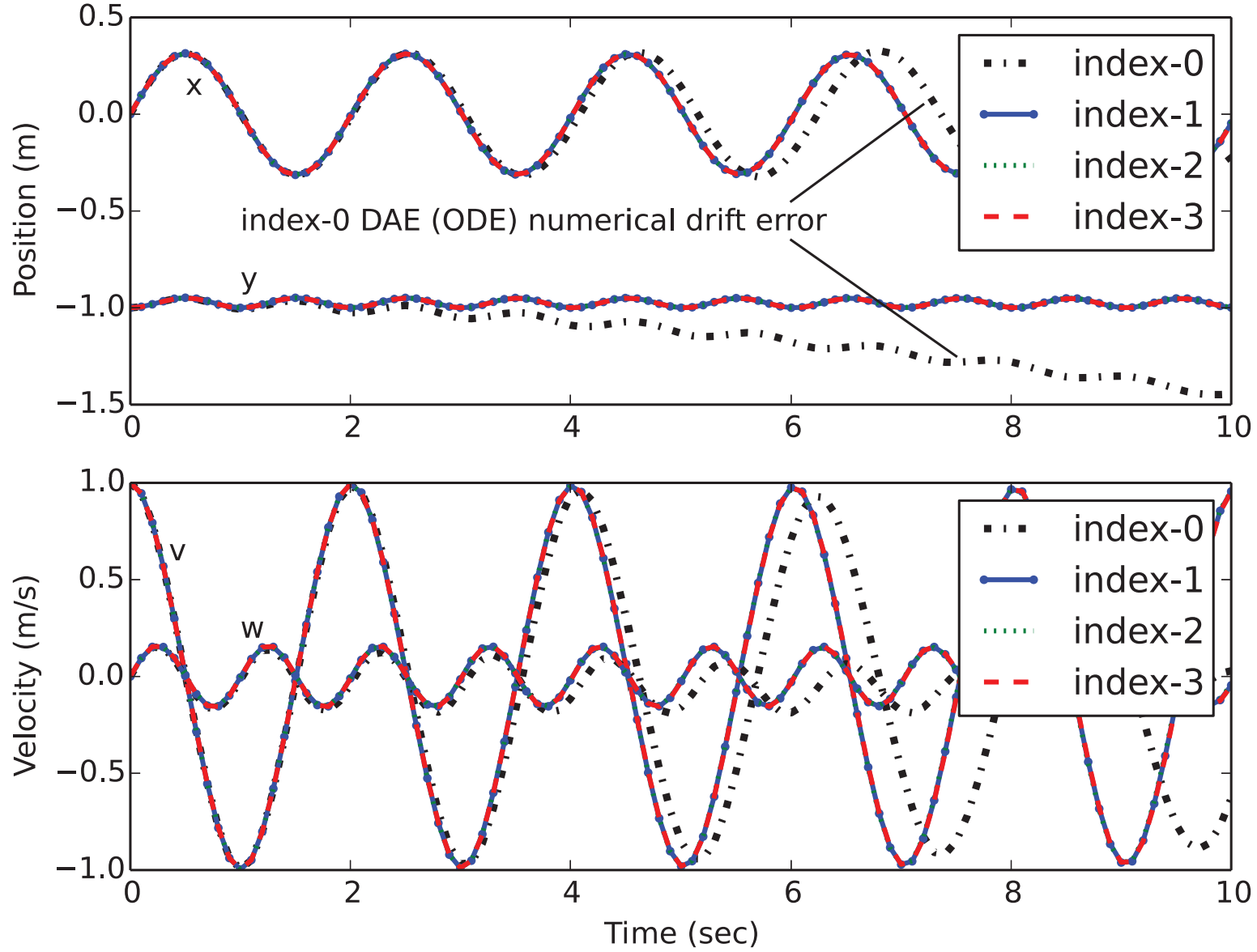
Index-0 DAE (ODE) Model
The differentiation of the equations (3 times) creates numerical drift in the solution, especially noticeable with lambda and y.
from gekko import GEKKO
import numpy as np
mass = 1
g = 9.81
s = 1
m = GEKKO()
x = m.Var(0)
y = m.Var(-s)
v = m.Var(1)
w = m.Var(0)
lam = m.Var(mass*(1+s*g)/2*s**2)
m.Equation(lam.dt()==(-4*lam*(x*v+y*w) - 1.5*g*mass*w)/(x**2+y**2))
m.Equation(x.dt()==v)
m.Equation(y.dt()==w)
m.Equation(mass*v.dt()==-2*x*lam)
m.Equation(mass*w.dt()==-mass*g - 2*y*lam)
m.time = np.linspace(0,2*np.pi,100)
m.options.IMODE=4
m.options.NODES=3
m.solve(disp=False)
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.subplot(3,1,1)
plt.plot(m.time,x.value,label='x')
plt.plot(m.time,y.value,label='y')
plt.ylabel('Position')
plt.legend(); plt.grid()
plt.subplot(3,1,2)
plt.plot(m.time,v.value,label='v')
plt.plot(m.time,w.value,label='w')
plt.ylabel('Velocity')
plt.legend(); plt.grid()
plt.subplot(3,1,3)
plt.plot(m.time,lam.value,label=r'$\lambda$')
plt.legend(); plt.grid()
plt.xlabel('Time')
plt.savefig('index0.png',dpi=600)
plt.show()
Model pend0
Parameters
m = 1
g = 9.81
s = 1
End Parameters
Variables
x = 0
y = -s
v = 1
w = 0
lam = m*(1+s*g)/2*s^2
End Variables
Equations
$lam = (-4*lam*(x*v+y*w) - 1.5*g*m*w)/(x^2+y^2)
$x = v
$y = w
m*$v = -2*x*lam
m*$w = -m*g - 2*y*lam
End Equations
End Model
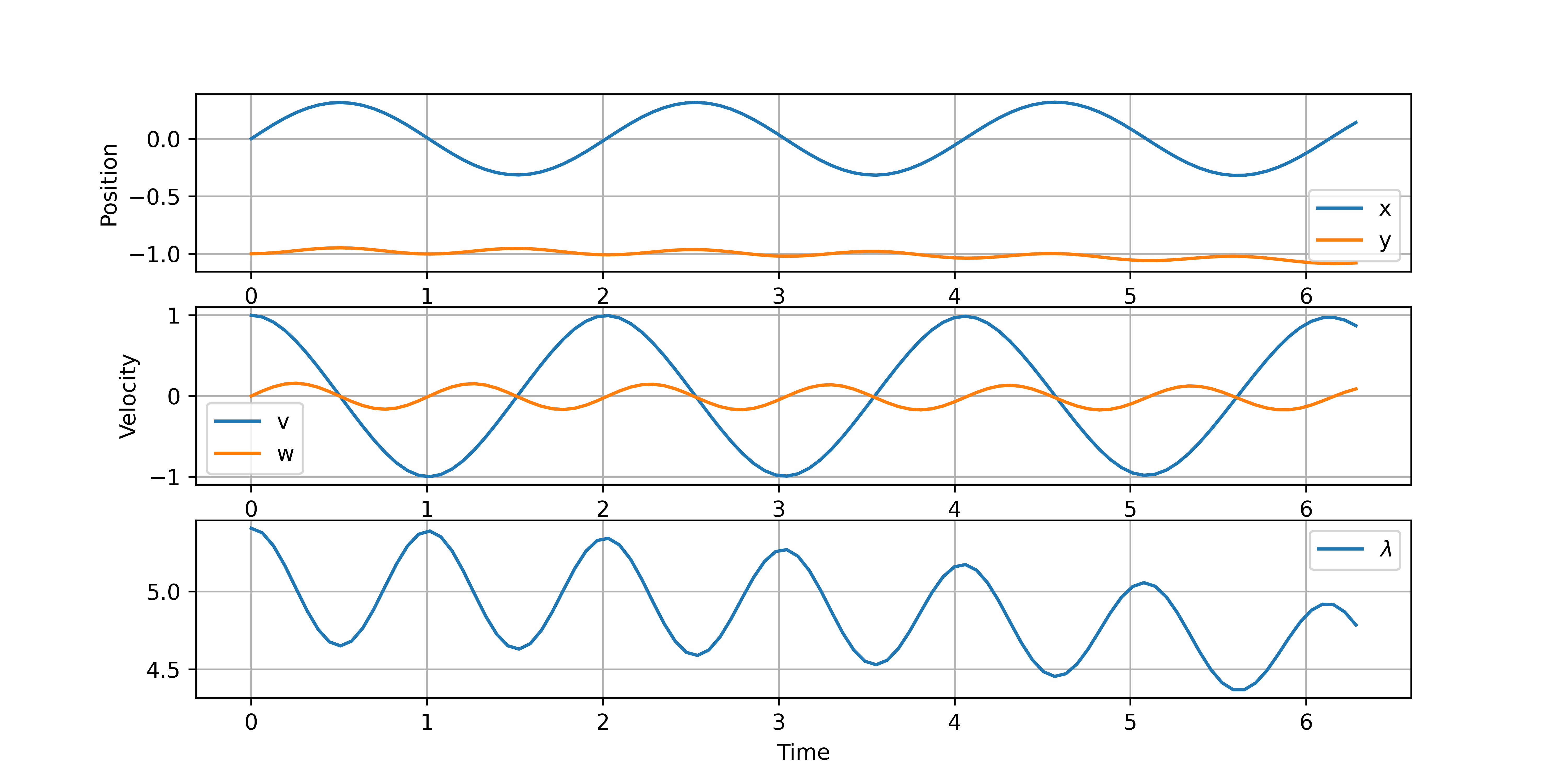
Index-1 DAE Model
There is less numerical drift with the index-1 form but the solution is still not sufficiently accurate.
from gekko import GEKKO
import numpy as np
mass = 1
g = 9.81
s = 1
m = GEKKO()
x = m.Var(0)
y = m.Var(-s)
v = m.Var(1)
w = m.Var(0)
lam = m.Var(mass*(1+s*g)/2*s**2)
m.Equation(mass*(v**2+w**2-g*y)-2*lam*(x**2+y**2)==0)
m.Equation(x.dt()==v)
m.Equation(y.dt()==w)
m.Equation(mass*v.dt()==-2*x*lam)
m.Equation(mass*w.dt()==-mass*g - 2*y*lam)
m.time = np.linspace(0,2*np.pi,100)
m.options.IMODE=4
m.options.NODES=3
m.solve(disp=False)
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.subplot(3,1,1)
plt.plot(m.time,x.value,label='x')
plt.plot(m.time,y.value,label='y')
plt.ylabel('Position')
plt.legend(); plt.grid()
plt.subplot(3,1,2)
plt.plot(m.time,v.value,label='v')
plt.plot(m.time,w.value,label='w')
plt.ylabel('Velocity')
plt.legend(); plt.grid()
plt.subplot(3,1,3)
plt.plot(m.time,lam.value,label=r'$\lambda$')
plt.legend(); plt.grid()
plt.xlabel('Time')
plt.savefig('index1.png',dpi=600)
plt.show()
Model pend1
Parameters
m = 1
g = 9.81
s = 1
End Parameters
Variables
x = 0
y = -s
v = 1
w = 0
lam = m*(1+s*g)/2*s^2
End Variables
Equations
m*(v^2+w^2-g*y) - 2*lam*(x^2+y^2) = 0
$x = v
$y = w
m*$v = -2*x*lam
m*$w = -m*g - 2*y*lam
End Equations
End Model
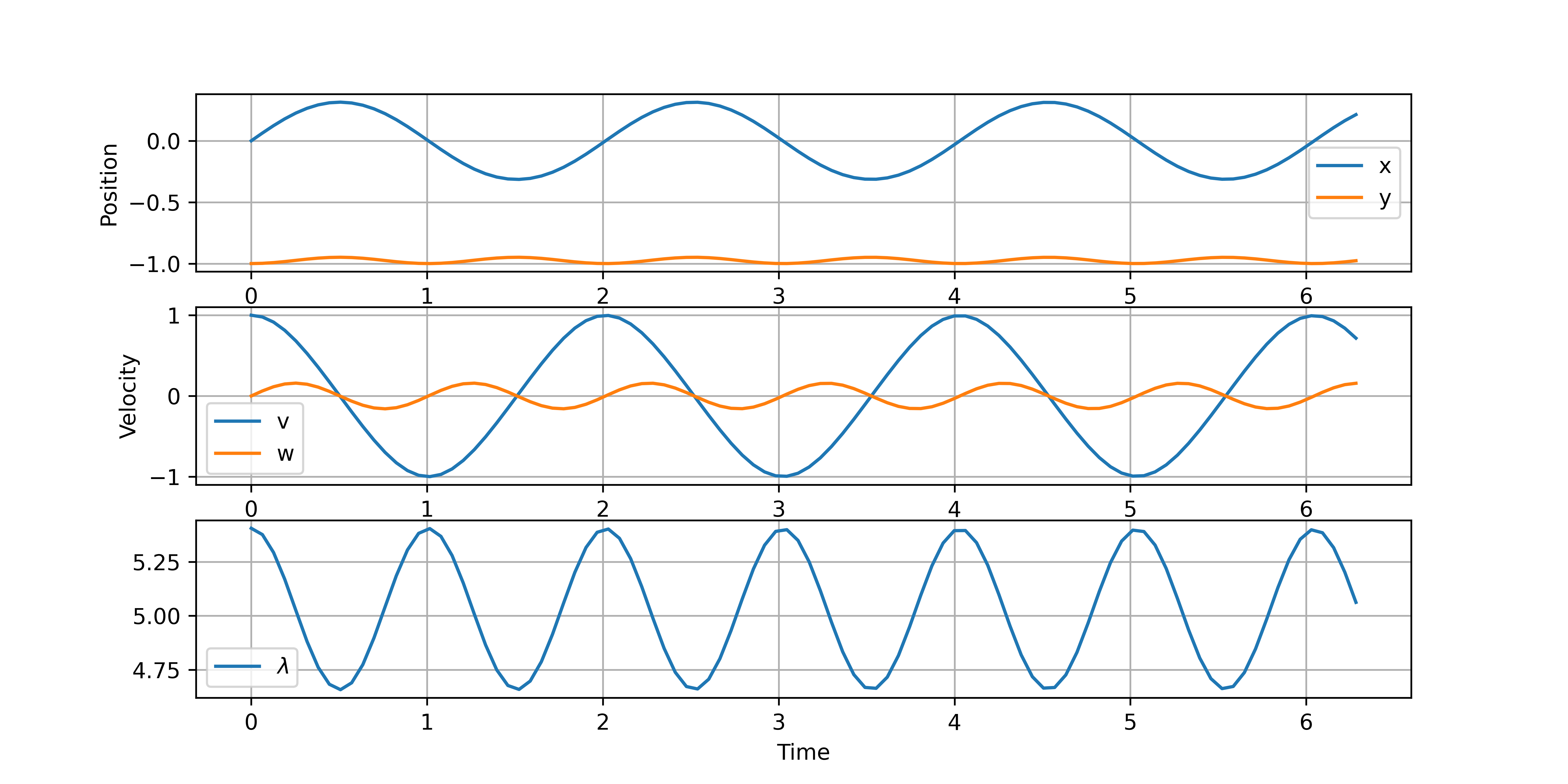
Index-2 DAE Model
Some DAE numerical methods can solve up to index-2 DAEs in Hessenberg form. This is not required with Gekko and APMonitor that can solve any index-2 or higher DAE form. The index-2 form has no numerical drift but is still not as desirable as index-3 form that requires no rearrangement.
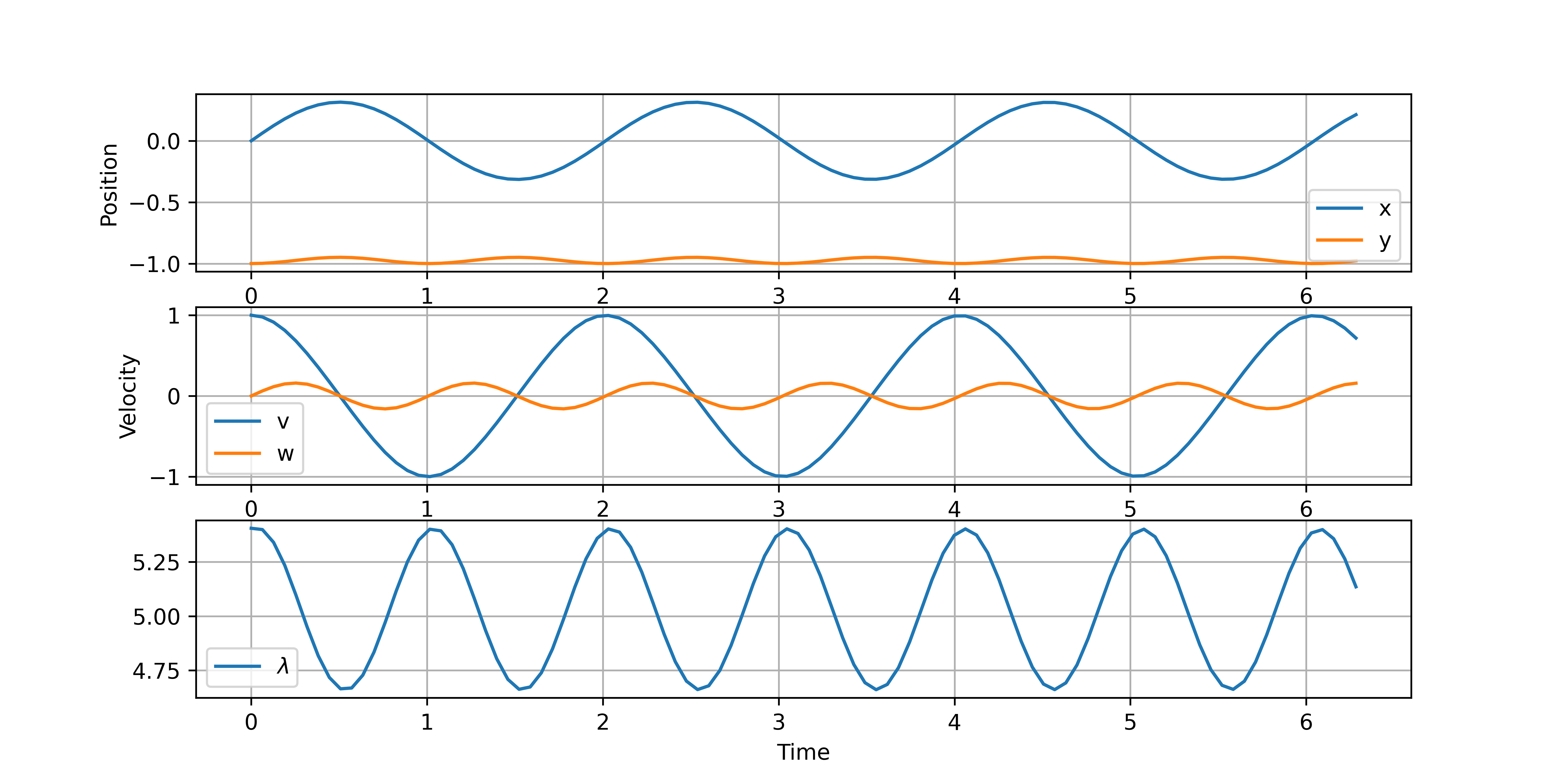
from gekko import GEKKO
import numpy as np
mass = 1
g = 9.81
s = 1
m = GEKKO()
x = m.Var(0)
y = m.Var(-s)
v = m.Var(1)
w = m.Var(0)
lam = m.Var(mass*(1+s*g)/2*s**2)
m.Equation(x*v + y*w==0)
m.Equation(x.dt()==v)
m.Equation(y.dt()==w)
m.Equation(mass*v.dt()==-2*x*lam)
m.Equation(mass*w.dt()==-mass*g-2*y*lam)
m.time = np.linspace(0,2*np.pi,100)
m.options.IMODE=4
m.options.NODES=3
m.solve(disp=False)
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.subplot(3,1,1)
plt.plot(m.time,x.value,label='x')
plt.plot(m.time,y.value,label='y')
plt.ylabel('Position')
plt.legend(); plt.grid()
plt.subplot(3,1,2)
plt.plot(m.time,v.value,label='v')
plt.plot(m.time,w.value,label='w')
plt.ylabel('Velocity')
plt.legend(); plt.grid()
plt.subplot(3,1,3)
plt.plot(m.time,lam.value,label=r'$\lambda$')
plt.legend(); plt.grid()
plt.xlabel('Time')
plt.savefig('index2.png',dpi=600)
plt.show()
Model pend2
Parameters
m = 1
g = 9.81
s = 1
End Parameters
Variables
x = 0
y = -s
v = 1
w = 0
lam = m*(1+s*g)/2*s^2
End Variables
Equations
x * v + y * w = 0
$x = v
$y = w
m*$v = -2*x*lam
m*$w = -m*g - 2*y*lam
End Equations
End Model
Index-3 DAE Model
The index-3 form requires no rearrangement and has no numerical drift associated with index reduction. APMonitor and Gekko solve high-index DAEs with orthogonal collocation on finite elements either in simultaneous or sequential modes. This also allows the DAEs to be solved in optimization problems versus only simulation.
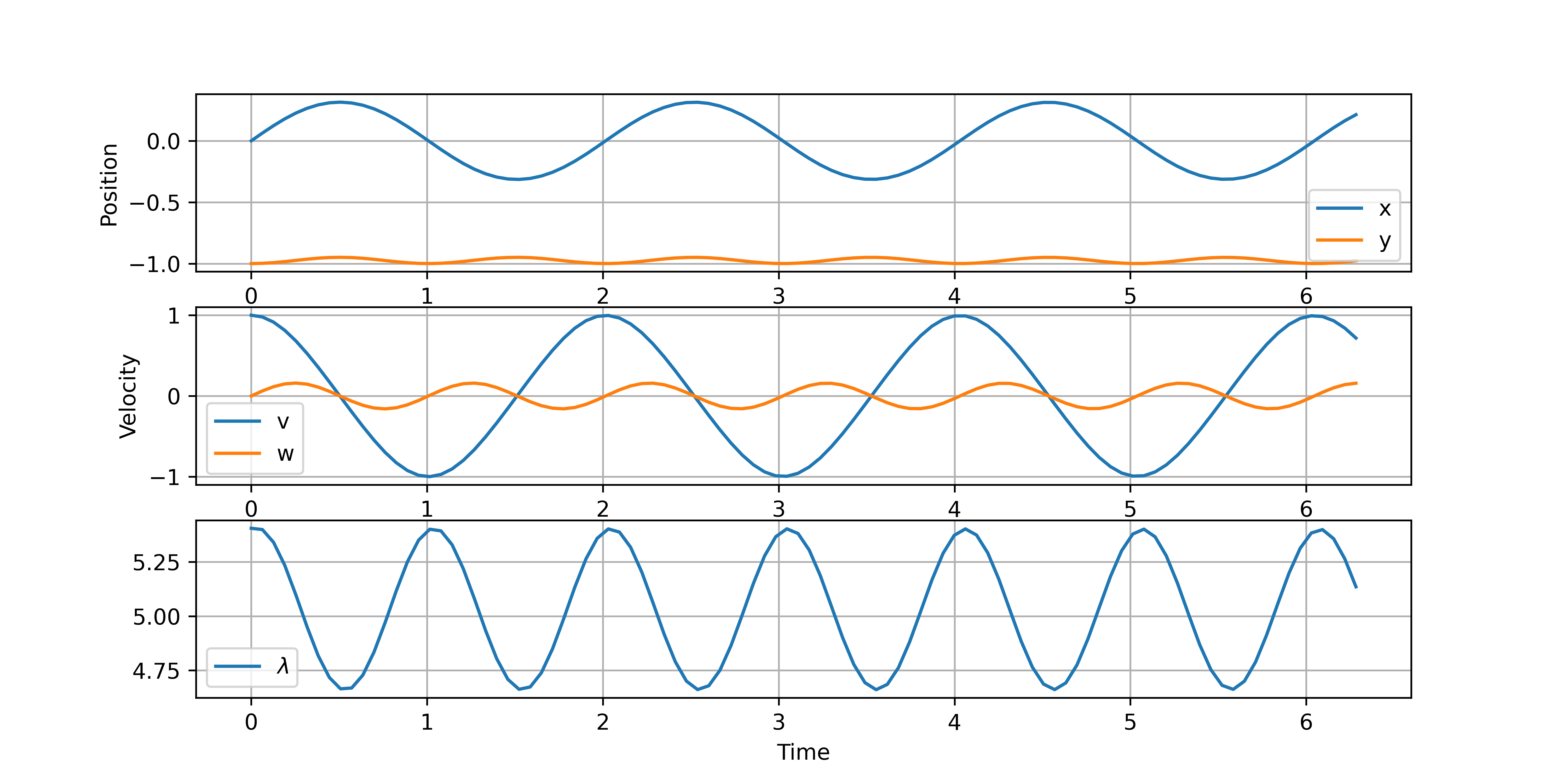
from gekko import GEKKO
import numpy as np
mass = 1
g = 9.81
s = 1
m = GEKKO()
x = m.Var(0)
y = m.Var(-s)
v = m.Var(1)
w = m.Var(0)
lam = m.Var(mass*(1+s*g)/2*s**2)
m.Equation(x**2+y**2==s**2)
m.Equation(x.dt()==v)
m.Equation(y.dt()==w)
m.Equation(mass*v.dt()==-2*x*lam)
m.Equation(mass*w.dt()==-mass*g-2*y*lam)
m.time = np.linspace(0,2*np.pi,100)
m.options.IMODE=4
m.options.NODES=3
m.solve(disp=False)
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.subplot(3,1,1)
plt.plot(m.time,x.value,label='x')
plt.plot(m.time,y.value,label='y')
plt.ylabel('Position')
plt.legend(); plt.grid()
plt.subplot(3,1,2)
plt.plot(m.time,v.value,label='v')
plt.plot(m.time,w.value,label='w')
plt.ylabel('Velocity')
plt.legend(); plt.grid()
plt.subplot(3,1,3)
plt.plot(m.time,lam.value,label=r'$\lambda$')
plt.legend(); plt.grid()
plt.xlabel('Time')
plt.savefig('index3.png',dpi=600)
plt.show()
Model pend3
Parameters
m = 1
g = 9.81
s = 1
End Parameters
Variables
x = 0
y = -s
v = 1
w = 0
lam = m*(1+s*g)/2*s^2
End Variables
Equations
x^2 + y^2 = s^2
$x = v
$y = w
m*$v = -2*x*lam
m*$w = -m*g - 2*y*lam
End Equations
End Model
See Inverted Pendulum Control and Crane Pendulum Modeling and Control
References
- Safdarnejad, S.M., Hedengren, J.D., Lewis, N.R., Haseltine, E., Initialization Strategies for Optimization of Dynamic Systems, Computers and Chemical Engineering, 2015, Vol. 78, pp. 39-50, DOI: 10.1016/j.compchemeng.2015.04.016 Article
