APMonitor

APM Python is designed for large-scale optimization and accesses solvers of constrained, unconstrained, continuous, and discrete problems. Problems in linear programming, quadratic programming, integer programming, nonlinear optimization, systems of dynamic nonlinear equations, and multiobjective optimization can be solved. The platform can find optimal solutions, perform tradeoff analyses, balance multiple design alternatives, and incorporate optimization methods into external modeling and analysis software. It is free for academic and commercial use.

Recommended: A newer Python interface is the GEKKO Optimization Suite that is available with:

  python pip install gekko

Instructions below are for working with the original APM Python package that requires an APM model and data files. The advantage of working with GEKKO is that the model equations and data are defined directly within the Python language instead of in separate files (see documentation). There is also an option to run locally in GEKKO without an Apache server for Linux and Windows. Both APM Python and GEKKO solve optimization problems on public servers by default and this option is available for all platforms (Windows, Linux, MacOS, ARM processors, etc) that run Python.

APM Python is designed for large-scale optimization and accesses solvers of constrained, unconstrained, continuous, and discrete problems. Problems in linear programming, quadratic programming, integer programming, nonlinear optimization, systems of dynamic nonlinear equations, and multiobjective optimization can be solved. The platform can find optimal solutions, perform tradeoff analyses, balance multiple design alternatives, and incorporate optimization methods into external modeling and analysis software. It is free for academic and commercial use. A newer Python interface is the GekkoPythonOptimizationGEKKO Optimization Suite? that is available with:

    python pip install gekko

Instructions below are for working with the original APM Python package that requires an APM model and data files. The advantage of working with GEKKO is that the model equations and data are defined directly within the Python language instead of in separate files (see documentation).

Another method to obtain APMonitor is to include the following code snippet at the beginning of a Python script. The installation is only required once and then the code can be commented or removed.

(:source lang=python:) try:

    from pip import main as pipmain

except:

    from pip._internal import main as pipmain

pipmain(['install','APMonitor'])

1. to upgrade: pipmain(['install','--upgrade','APMonitor'])

(:sourceend:)

The Dynamic Optimization Course is graduate level course taught over 14 weeks to introduce concepts in mathematical modeling, data reconciliation, estimation, and control. There are many other applications and instructional material posted to this freely available course web-site.

    from APMonitor.apm import *

    from APMonitor.apm import *

    from apm import *

    from apm import *

APM Python is designed for large-scale optimization and accesses solvers of constrained, unconstrained, continuous, and discrete problems. Problems in linear programming, quadratic programming, integer programming, nonlinear optimization, systems of dynamic nonlinear equations, and multiobjective optimization can be solved. The platform can find optimal solutions, perform tradeoff analyses, balance multiple design alternatives, and incorporate optimization methods into external modeling and analysis software. It is free for academic and commercial use.

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/WF3iieZfRA0" frameborder="0" allowfullscreen></iframe> (:htmlend:)

Example applications of nonlinear models with differential and algebraic equations are available for download below or from the following GitHub repository.

The development roadmap for this and other libraries are detailed in the release notes. The zipped archive contains the APM Python library apm.py and a number of example problems in separate folders. Descriptions of some of the example problems are provided below.

Another method to obtain APMonitor is to include the following code snippet at the beginning of a Python script. If APMonitor is not available, it will use the pip module to install it.

 try:

 except:

    pip.main(['install','APMonitor'])

(:source lang=python:) try:

    from APMonitor import *

except:

    # Automatically install APMonitor
    import pip
    def install(package):
        pip.main(['install', package])
    # Example
    if __name__ == _main_:
        install('APMonitor')
    from APMonitor import *

(:sourceend:)

$$ \mathrm{subject\;to} \quad x_1 x_2 x_3 x_4 \ge 25$$

$$ s.t. x_1 x_2 x_3 x_4 \ge 25$$

$$\quad x_1^2 + x_2^2 + x_3^2 + x_4^2 = 40$$

$$\quad 1 \le x_1, x_2, x_3, x_4 \le 5$$

$$\quad x_0 = (1,5,5,1)$$

$$ \min x_1 x_4 (x_1 + x_2 + x_3) + x_3 $$ $$ s.t. x_1 x_2 x_3 x_4 /ge 25$$ $$ x_1^2 + x_2^2 + x_3^2 + x_4^2 = 40$$ $$ 1 \le x_1, x_2, x_3, x_4 \le 5$$

$$ x_0 = (1,5,5,1)$$

$$ \min \, x_1 x_4 (x_1 + x_2 + x_3) + x_3 $$

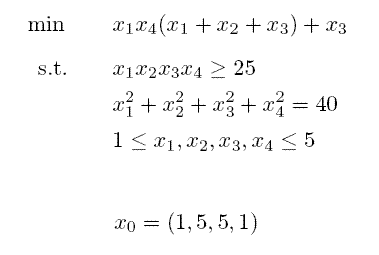
$$ /min /, x_1 x_4 \left(x_1 + x_2 + x_3 \right) + x_3 $$

The APMonitor package is also available through the package manager pip in Python.

 python pip install APMonitor

The latest APM Python libraries are attached below. Functionality has been tested with Python 2.7 and 3.5. Example applications that use the apm.py library are listed further down on this page.

Download APM Python (version 0.7.2) - Released 19 Feb 2016

 git clone git://github.com/APMonitor/apm_python

• APM IPython Notebook Example on GitHub

(:title Python Optimization Package:)

• Solve this optimization problem from a web-browser interface or download the Python source above. The Python files are contained in folder example_hs71.

Solve this problem problem from a web-browser interface.

• APM Python Source Code Documentation

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/t84YMw8p34w?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)