Box Folding Optimization
Main.BoxFolding History
Hide minor edits - Show changes to markup
Test your knowledge with a Quiz on Box Folding Optimization
(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)
m.Obj(Volume) # how to maximize Volume?
m.Maximize(Volume)
(:source lang=python:) from gekko import GEKKO m = GEKKO() tabs = 5.0 / 100 # m = cm * (1m/100cm) Area = 0.8 # m^2 w = m.Var(lb=0) # width of the cardboard piece x = m.Var(lb=0) # length of cut-out h = m.Intermediate(Area / w) # Area = w h box_width = m.Intermediate(w - 2 * x) box_length = m.Intermediate(h - 2 * x) box_height = m.Intermediate(x) box_width_with_tabs = m.Intermediate(box_width + 2 * tabs) Volume = m.Intermediate(box_width * box_length * box_height)
- upper constraint for box width with tabs
m.Equation(box_width_with_tabs < w)
- lower constraint for box width with tabs
m.Equations([box_width > 0,box_length > 0,Volume>0.01]) m.Obj(Volume) # how to maximize Volume? m.solve() print('width = ' + str(w.value[0])) print('length = ' + str(h.value[0])) print('height = ' + str(x.value[0])) print('volume = ' + str(Volume.value[0])) (:sourceend:)
A piece of cardboard with a total area of 0.8m2 is to be made into an open-top box by first removing the corners and then by folding the box sides up and securing the tabs to the adjacent box side. The starting cardboard sheet has height h and width w. When cut and folded, the box has a width of w-2x, a length of h-2x, and a height of x. In order to properly secure the tabs to the adjacent box side, the width of the tab must be 5 centimeters (0.05m). The objective is to maximize the volume of the box by choosing an appropriate value of x (the height of the box) and w (the starting width of the cardboard sheet).
A piece of cardboard with a total area of 0.8m2 is to be made into an open-top box by first removing the corners and then by folding the box sides up and securing the tabs to the adjacent box side. The starting cardboard sheet has height h and width w. When cut and folded, the box has a width of w-2x, a length of h-2x, and a height of x. In order to properly secure the tabs to the adjacent box side, the width of the tab must be 5 centimeters (0.05m). The objective is to maximize the volume of the box by choosing an appropriate value of x (the height of the box) and w (the starting width of the cardboard sheet).
(:title Box Folding Optimization:) (:keywords box folding, project, nonlinear, optimization, engineering optimization, engineering design, interior point, active set, circle packing, packing optimization, python, matlab:) (:description An optimization application to determine the maximum size of a box from a 0.8m^2 piece of cardboard.:)
Box Folding Optimization
A piece of cardboard with a total area of 0.8m2 is to be made into an open-top box by first removing the corners and then by folding the box sides up and securing the tabs to the adjacent box side. The starting cardboard sheet has height h and width w. When cut and folded, the box has a width of w-2x, a length of h-2x, and a height of x. In order to properly secure the tabs to the adjacent box side, the width of the tab must be 5 centimeters (0.05m). The objective is to maximize the volume of the box by choosing an appropriate value of x (the height of the box) and w (the starting width of the cardboard sheet).
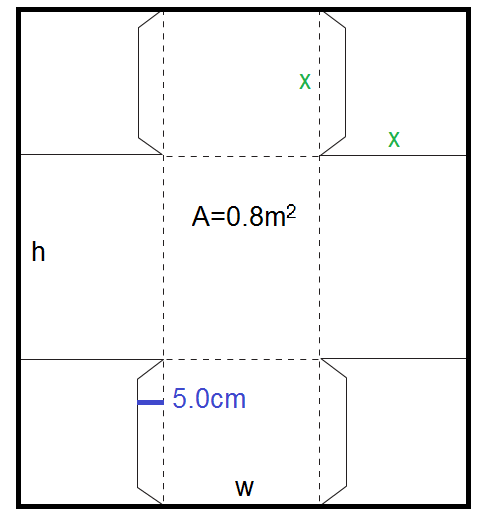
Box Folding Problem Box Folding Solution
Download Sample Python Code
Python source code solves the box optimization problem with Newton's method, a quasi-Newton's method (BFGS), a steepest descent approach, and a conjugate gradient method. After the script executes, a figure appears that shows a contour plot of the solution with a graphical depiction of the progress of each method.
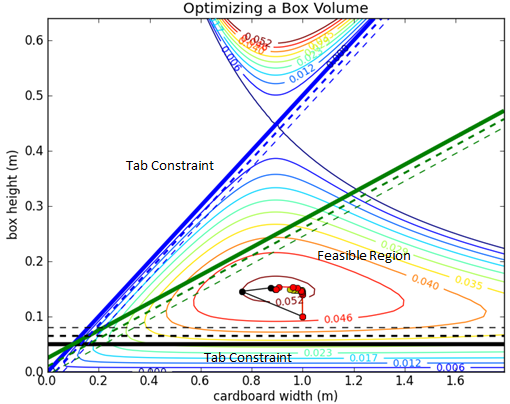
(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)

