Design Optimization

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/rAoDhuOpPf0" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)

A slurry pipeline transports a mixture of materials suspended in a liquid or gas. These materials are usually particles of solid matter, such as sand, clay, and other minerals, suspended in a liquid base, such as water or oil. Slurry pipelines are used in many industries, including mining, oil and gas, and agriculture.

ffp = True if ffp:

    y = m.Intermediate(m.log(Rw))
    fw = m.Intermediate(-1.5919e-4*y**3+5.5535e-3*y**2                        -6.8029e-2*y+0.31078)

else:

    fw1 = 0.3164/(Rw**0.25)
    fw2 = 0.0032+0.221*Rw**-0.237
    fw = m.if3(Rw-1e5,fw1,fw2)

import numpy as np

Rw = m.Intermediate(rho_w*V*Dpipe/mu)

1. Friction factor

y = m.Intermediate(m.log(Rw))

cspline = True

if cspline:

    # Optimal Power: 286164
    import pandas as pd
    course = 'http://apmonitor.com/me575/'
    url = 'index.php/Main/LimestoneSlurry'
    data = pd.read_html(course+url)[0] # read data
    lnCdRp2,lnCd,Cd = m.Array(m.Var,3,value=2)
    m.Equation(m.exp(lnCdRp2)==CdRp2)
    m.Equation(m.exp(lnCd)==Cd)
    m.cspline(lnCdRp2,lnCd,
              np.log(data['CdRp2'].values),
              np.log(data['Cd'].values),False)

else:

    # Optimal Power: 276570
    x = m.Intermediate(m.log(CdRp2))
    Cd = m.Intermediate(m.exp(0.03420*x**2                              -0.98327*x+6.17176))

m.options.SOLVER=1

        <th><b>CdRp2</b></th>
        <th><b>Cd</b></th>

        <td><b>CdRp2</b></td>
        <td><b>Cd</b></td>

Part of the optimization model requires an empirical model of C_d vs. C_dR_p² to correctly size the slurry pump. There are several methods for obtaining a regression model of this relationship including a cubic spline or machine learning regression methods. Gekko (see documentation) imports TensorFlow, Scikit-Learn, and Gaussian Process models.

(:sourceend:)

(:html:) <style type="text/css"> div.table-title {

   display: block;
  margin: auto;
  max-width: 600px;
  padding:5px;
  width: 100%;

}

.table-title h3 {

   color: #fafafa;

}

.table-fill {

  background: white;
  border-radius:3px;
  border-collapse: collapse;
  height: 320px;
  margin: auto;
  max-width: 600px;
  padding:5px;
  width: 100%;
  box-shadow: 0 5px 10px rgba(0, 0, 0, 0.1);
  animation: float 5s infinite;

}

th {

  color:#D5DDE5;;
  background:#1b1e24;
  border-bottom:4px solid #9ea7af;
  border-right: 1px solid #343a45;
  text-align:left;
  vertical-align:middle;

}

th:first-child {

  border-top-left-radius:3px;

}

th:last-child {

  border-top-right-radius:3px;
  border-right:none;

}

tr {

  border-top: 1px solid #C1C3D1;
  border-bottom-: 1px solid #C1C3D1;
  color:#666B85;
  font-weight:normal;

}

tr:hover td {

  border-top: 1px solid #22262e;
  border-bottom: 1px solid #22262e;

}

tr:first-child {

  border-top:none;

}

tr:last-child {

  border-bottom:none;

}

tr:nth-child(odd) td {

  background:#EEEEEE;

}

tr:last-child td:first-child {

  border-bottom-left-radius:3px;

}

tr:last-child td:last-child {

  border-bottom-right-radius:3px;

}

td {

  background:#FFFFFF;
  padding:5px;
  text-align:left;
  vertical-align:middle;
  border-right: 1px solid #C1C3D1;

}

td:last-child {

  border-right: 0px;

}

th.text-left {

  text-align: left;

}

th.text-center {

  text-align: center;

}

th.text-right {

  text-align: right;

}

td.text-left {

  text-align: left;
  width: 45%;

}

td.text-center {

  text-align: center;
  width: 10%;

}

td.text-small {

  text-align: center;
  width: 10%;

}

td.text-right {

  text-align: right;

} </style> (:htmlend:)

(:html:) <table>

    <tr>
        <td>CdRp2</td>
        <td>Cd</td>
    </tr>
    <tr>
        <td>2.4</td>
        <td>240</td>
    </tr>
    <tr>
        <td>4.8</td>
        <td>120</td>
    </tr>
    <tr>
        <td>7.2</td>
        <td>80</td>
    </tr>
    <tr>
        <td>12.4</td>
        <td>49.5</td>
    </tr>
    <tr>
        <td>17.9</td>
        <td>36.5</td>
    </tr>
    <tr>
        <td>26.5</td>
        <td>26.5</td>
    </tr>
    <tr>
        <td>58.4</td>
        <td>14.6</td>
    </tr>
    <tr>
        <td>93.7</td>
        <td>10.4</td>
    </tr>
    <tr>
        <td>173</td>
        <td>6.9</td>
    </tr>
    <tr>
        <td>260</td>
        <td>5.3</td>
    </tr>
    <tr>
        <td>410</td>
        <td>4.1</td>
    </tr>
    <tr>
        <td>1020</td>
        <td>2.55</td>
    </tr>
    <tr>
        <td>1800</td>
        <td>2</td>
    </tr>
    <tr>
        <td>3750</td>
        <td>1.5</td>
    </tr>
    <tr>
        <td>6230</td>
        <td>1.27</td>
    </tr>
    <tr>
        <td>10,700</td>
        <td>1.07</td>
    </tr>
    <tr>
        <td>30,800</td>
        <td>0.77</td>
    </tr>
    <tr>
        <td>58,500</td>
        <td>0.65</td>
    </tr>
    <tr>
        <td>138,000</td>
        <td>0.55</td>
    </tr>
    <tr>
        <td>245,000</td>
        <td>0.5</td>
    </tr>
    <tr>
        <td>460,000</td>
        <td>0.46</td>
    </tr>
    <tr>
        <td>1,680,000</td>
        <td>0.42</td>
    </tr>
    <tr>
        <td>3,600,000</td>
        <td>0.4</td>
    </tr>
    <tr>
        <td>9,600,000</td>
        <td>0.385</td>
    </tr>

</table> (:htmlend:)

1. Slurry Pipeline

L = 15*5280 # Length of pipeline (ft) W = 12.67 # Massflow of limestone (lbm/sec) a = 0.01 # Average lump-size before grinding (ft) pi = 3.1415927

rho_w = 62.428 # Density of water (lbm/ft^3) mu = 7.392e-4 # Viscosity of water (lbm/ft/sec) g = 32.174 # Gravitational constant (ft/sec^2)

gc = 32.174049

gamma_L = 168.5

V = m.Var(value=10, lb=1, ub=20, name='V')

1. Volumetric concentration of slurry
2. (Vol limestone/Vol Total)

c = m.Var(value=0.2, lb=0.01, ub=0.4, name='c')

Dpipe = m.Var(value=0.4, lb=0.01, ub=0.5, name='Dpipe')

d = m.Var(value=0.008, lb=0.0008, name='d') Pt = m.Var(value=1, name='Pt')

fw = m.Intermediate(-1.5919e-4*y**3+5.5535e-3*y**2 -6.8029e-2*y+0.31078)

CdRp2 = m.Intermediate(4*g*rho_w*d**3* (gamma_L-rho_w)/(3*mu**2)) x = m.Intermediate(m.log(CdRp2)) Cd = m.Intermediate(m.exp(0.03420*x**2-0.98327*x+6.17176))

rho = m.Intermediate((1-c)*rho_w+c*gamma_L)

S = m.Intermediate(gamma_L/rho_w)

r = m.Intermediate(rho_w/rho) t = m.Intermediate(g*Dpipe*(S-1)/(V**2*m.sqrt(Cd))) f = m.Intermediate(fw*(r+150*c*r*t**1.5))

dp = m.Intermediate(f*rho*L*V**2/(2*Dpipe*gc))

Area = m.Intermediate(pi*Dpipe**2/4)

Q = m.Intermediate(Area*V)

mdot = m.Intermediate(rho*Area*V)

Q_L = m.Intermediate(Q*c) # ft^3/sec

1. lbm/sec = (lbm/ft^3) * (ft^3/sec)

mdot_L = m.Intermediate(gamma_L*Q_L)

Pf = m.Intermediate(dp*Q)

Pg = m.Intermediate(218*W*(1/m.sqrt(d)-1/m.sqrt(a)))

Vc = m.Intermediate((40*g*c*(S-1)*Dpipe/m.sqrt(Cd))**0.5)

1. Velocity must be greater than
2. the critical velocity constraint

(:description Engineering design and optimization of limestone slurry pipeline. Optimization principles are used to design the system.:)

(:title Limestone Slurry Pipeline Optimization:)

A slurry pipeline is a type of pipeline used to transport a mixture of materials suspended in a liquid or gas. These materials are usually particles of solid matter, such as sand, clay, and other minerals, suspended in a liquid base, such as water or oil. Slurry pipelines are used in many industries, including mining, oil and gas, and agriculture.

The optimization of a slurry pipeline depends on the type of slurry and the application. In general, the goal is to minimize the total cost of the pipeline, which includes capital and operating costs. Optimization may involve adjusting the diameter of the pipeline, the type and number of pumps, the use of valves and other controlling devices, and the installation of strainers and other equipment to filter out solids. Other considerations include the environmental impact of the pipeline, safety, and the ability to handle the slurry without damage to the equipment. In some cases, the optimization process may also include the use of additives to improve the flow characteristics of the slurry.

1. Conversion between lbm and lbf (lbm ft / lbf / s^2)

gc = m.Const(32.174049,'gc')

1. Density of limestone (lbm/ft^3)

gamma_L = m.Const(168.5,'gamma_L')

1. Average flow velocity (ft/sec)

V = m.Var(value=10 , lb=1 , ub=20 , name='V')

1. Volumetric concentration of slurry (Vol limestone/Vol Total)

c = m.Var(value=0.2 , lb=0.01 , ub=0.4 , name='c')

1. Internal pipe diameter (ft)

Dpipe = m.Var(value=0.4 , lb=0.01 , ub=0.5 , name='Dpipe')

1. Average particle size after grinding (ft)

d = m.Var(value=0.008 , lb=0.0008 , name='d')

(:sourceend:)

Solution Help

See GEKKO documentation and additional example problems.

(:source lang=python:) from gekko import GEKKO m = GEKKO()

1. Pipeline slurry
2. Constants

L = m.Const(15*5280,'L') # Length of pipeline (ft) W = m.Const(12.67,'W') # Massflow of limestone (lbm/sec) a = m.Const(0.01,'a') # Average lump-size before grinding (ft) pi = m.Const(3.1415927,'pi') # pi

rho_w = m.Const(62.428,'rho_w') # Density of water (lbm/ft^3) mu = m.Const(7.392e-4,'mu') # Viscosity of water (lbm/ft/sec) g = m.Const(32.174,'g') # Gravitational constant (ft/sec^2) gc = m.Const(32.174049,'gc') # Converstion between lbm and lbf (lbm ft / lbf / s^2) gamma_L = m.Const(168.5,'gamma_L') # Density of limestone (lbm/ft^3)

1. Variables

V = m.Var(value=10 , lb=1 , ub=20 , name='V') # Average flow velocity (ft/sec) c = m.Var(value=0.2 , lb=0.01 , ub=0.4 , name='c') # Volumetric concentration of slurry (Vol limestone/Vol Total) Dpipe = m.Var(value=0.4 , lb=0.01 , ub=0.5 , name='Dpipe') # Internal pipe diameter (ft) d = m.Var(value=0.008 , lb=0.0008 , name='d') # Average particle size after grinding (ft) Pt = m.Var(value=1 , name='Pt')

1. Intermediates
2. Reynolds number

Rw = m.Intermediate(rho_w*V*Dpipe/mu,'Rw')

1. Friction factor for water (fit empirical correlation)

y = m.Intermediate(m.log(Rw),'y') fw = m.Intermediate(-1.5919e-4*y**3+5.5535e-3*y**2-6.8029e-2*y+0.31078,'fw')

1. Dimensionless numbers to obtain drag coefficient

CdRp2 = m.Intermediate(4*g*rho_w*d**3*(gamma_L-rho_w)/(3*mu**2),'CdRp2') x = m.Intermediate(m.log(CdRp2),'x') Cd = m.Intermediate(m.exp(0.03420*x**2-0.98327*x+6.17176),'Cd')

1. Slurry density

rho = m.Intermediate((1-c)*rho_w+c*gamma_L,'rho')

1. Limestone specific gravity

S = m.Intermediate(gamma_L/rho_w,'S')

1. Slurry friction factor

r = m.Intermediate(rho_w/rho,'r') t = m.Intermediate(g*Dpipe*(S-1)/(V**2*m.sqrt(Cd)),'t') f = m.Intermediate(fw*(r+150*c*r*t**1.5),'f')

1. Pressure drop (lbf / ft^2)

dp = m.Intermediate(f*rho*L*V**2/(2*Dpipe*gc),'dp')

1. Pipe cross-sectional area (ft^2)

Area = m.Intermediate(pi*Dpipe**2/4,'Area')

1. Slurry flow rate (ft^3/sec)

Q = m.Intermediate(Area*V,'Q')

1. Slurry mass flow rate (lbm/sec)

mdot = m.Intermediate(rho*Area*V,'mdot')

1. Limestone mass flow rate (lbm/sec)

Q_L = m.Intermediate(Q*c,'Q_L') # ft^3/sec mdot_L = m.Intermediate(gamma_L*Q_L,'mdot_L') # lbm/sec = (lbm/ft^3) * (ft^3/sec)

1. Friction power loss (ft * lbf / sec)

Pf = m.Intermediate(dp*Q,'Pf')

1. Grinding power (ft*lbf/sec)

Pg = m.Intermediate(218*W*(1/m.sqrt(d)-1/m.sqrt(a)),'Pg')

1. Critical velocity

Vc = m.Intermediate((40*g*c*(S-1)*Dpipe/m.sqrt(Cd))**0.5,'Vc')

1. Equations
2. Total power (grinding + pumping)

m.Equation(Pt==Pg+Pf)

1. Mass flow of limestone

m.Equation(mdot_L==W)

1. Velocity must be greater than the critical velocity constraint

m.Equation(V>Vc)

m.Minimize(Pt)

m.solve() print('Optimal Power: ' + str(Pt[0])) (:sourceend:)

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/3bWc9RmxCPQ?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)

• Full Slurry Pipeline Assignment
• Slurry Pipeline Data for C_d vs. C_dR_p² in Excel

Slurry Pipeline Data for C_d vs. C_dR_p² in Excel

This assignment can be completed in groups of two. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.

(:html:)

 <div id="disqus_thread"></div>
    <script type="text/javascript">
        /* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
        var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname

        /* * * DON'T EDIT BELOW THIS LINE * * */
        (function() {
            var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
            dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
            (document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
        })();
    </script>
    <noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
    <a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>

(:htmlend:)

(:title Limestone Slurry Pipeline Optimization Problem:) (:keywords mining, slurry, pipeline, nonlinear, optimization, engineering optimization, two-bar optimization, engineering design, interior point, active set, differential, algebraic, modeling language, university course:) (:description Engineering design and optimization of a heat pump system for pasteurization of milk. Optimization principles are used to design the system.:)

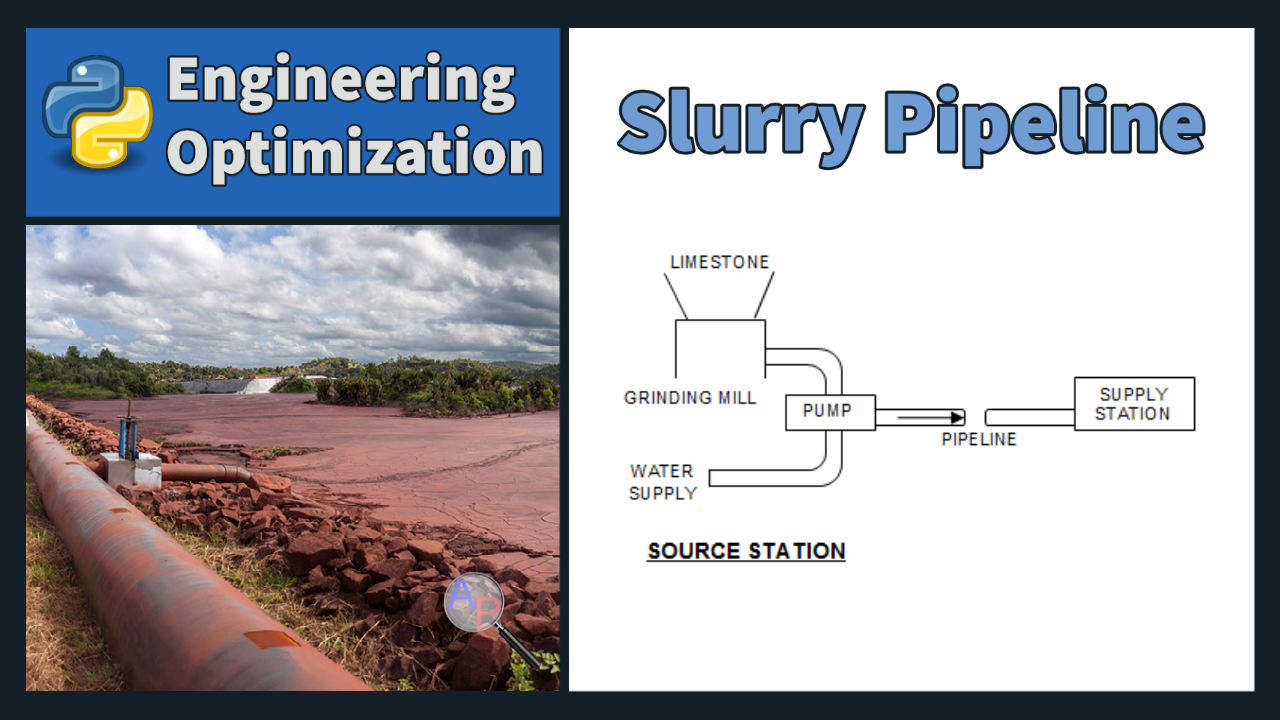
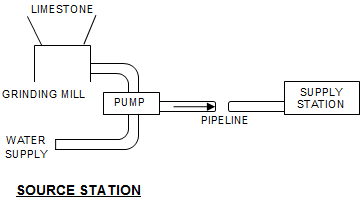
Design a pipeline for transporting crushed limestone from a quarry to a terminal located some distance away, using water as a transporting medium.

Full Slurry Pipeline Assignment

The limestone is crushed at the quarry, mixed with water to form a slurry, and pumped through the pipe. We would like to minimize the operating cost, which is primarily determined by the grinding power and the pumping power.

This problem is taken from James Siddall, Optimal Engineering Design, Dekker.

This assignment can be completed in groups of two. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.