Design Optimization

📄 A. Wächter and L. T. Biegler, On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming, Mathematical Programming 106(1), pp. 25-57, 2006. Download PDF

Interior Point Methods are a class of algorithms designed to solve optimization problems. They are used to find the optimal solution of a mathematical optimization problem by moving from one point on the objective function to another point in the interior of the feasible region. Interior Point Methods are often used to solve linear programming problems and can also be used to solve nonlinear programming problems. They typically employ a two-phase approach, with a first phase to find a feasible solution and the second phase to refine the solution to optimality. Interior Point Methods are generally more powerful and efficient than traditional methods, such as the simplex algorithm.

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/zm4mfr-QT1E" frameborder="0" allowfullscreen></iframe> (:htmlend:)

• MATLAB Code for Example 4

(:html:) <iframe width="560" height="315" src="//www.youtube.com/embed/oVqpaZB48eM?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)

• MATLAB Code for Example 3

• Interior Point Method Example 3 MATLAB Code

• Homework Problem 2 MATLAB Solution with BPOPT Solver
• Homework Problem 2 Online Solution with IPOPT Solver

• Problem 2 MATLAB Solution with BPOPT Solver
• Problem 2 Online Solution with IPOPT Solver

• Interior Point Method Lecture Notes

Interior Point Homework

Two exercises involve setting up and solving nonlinear programming problems with the interior point method.

• Interior Point Method Homework

The following animations demonstrate how the barrier term influences the objective contours. As the value of the barrier term (mu) decreases, the contours of the barrier problem approach the original objective contours.

• Interior Point Method Example 1
• Interior Point Method Example 2
• Interior Point Method Example 3
• Interior Point Method Example 4

Interior point methods are best suited for very large-scale problems with many degrees of freedom (design variables). Interior point methods are also relatively simple to code into a mathematical program. We will work with interior point methods to investigate the algorithmic details of constrained optimization.

The difficulty of the last few assignments has been reduced to allow time for work on the Final Project. Please use the additional time this week to develop your project.

Additional Interior Point Exercises

Interior Point Exercises

Two exercises involve setting up and solving nonlinear programming problems with the interior point method. The following animations demonstrate how the barrier term influences the objective contours. As the value of the barrier term (mu) decreases, the contours of the barrier problem approach the original objective contours.

• Interior Point Method Worksheet

• Source Code for this Animated Contour Plot with Python on Windows OS

• Source Code for this Animated Contour Plot with Python on Windows OS

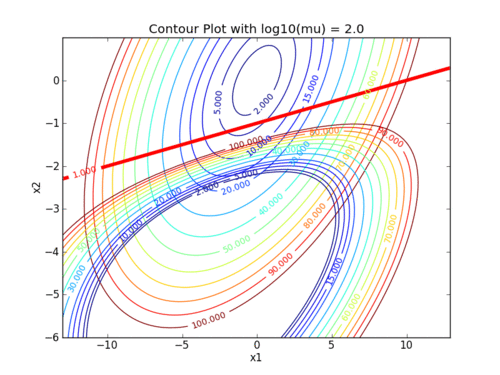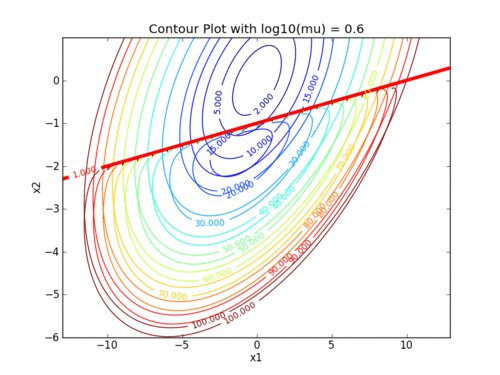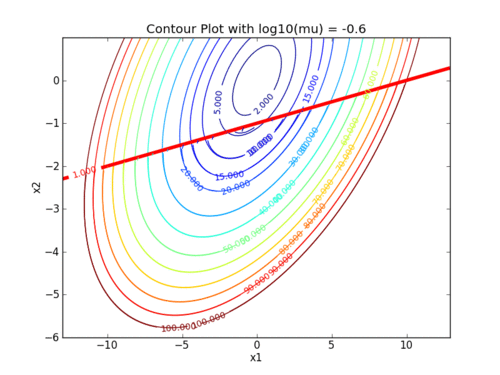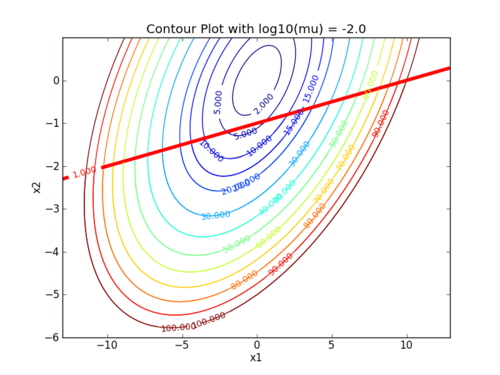
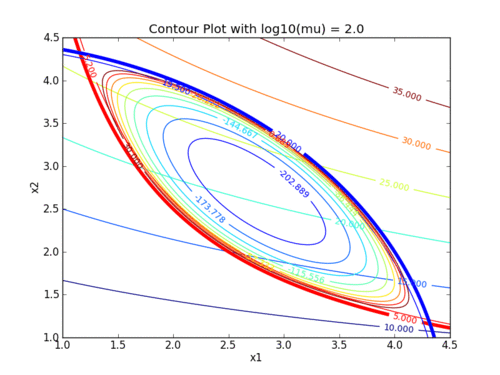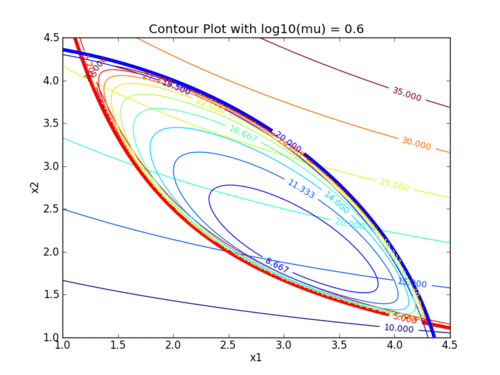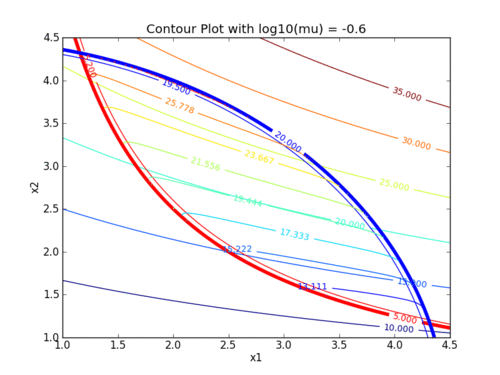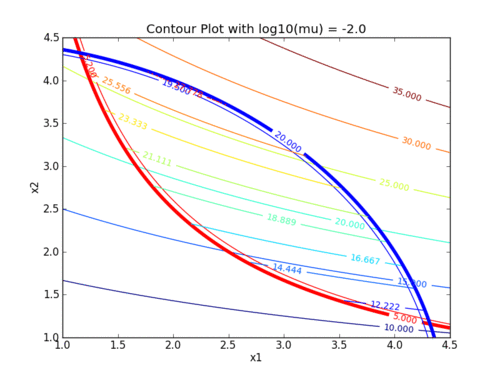
Interior point methods are best suited for very large-scale problems with many degrees of freedom (design variables). Interior point methods are also the simplest to code into a mathematical program. We will work with interior point methods to investigate the algorithmic details of constrained optimization.

1. A. Wächter and L. T. Biegler, On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming, Mathematical Programming 106(1), pp. 25-57, 2006. Download PDF

• Interior Point Method Notes

• Create an Animated Contour Plot with Python on Windows OS

• Create An Animated Contour Plot with Python on Windows OS

• Create An Animated Contour Plot in Windows

The difficulty of the last few assignments has been reduced to allow time for work on the Final Project. Please use the additional time this week to develop a project scope.

(:title Interior Point Methods:) (:keywords Interior Point Method, Lagrange Multiplier, Optimization, Constraint, Nonlinear Programming:) (:description Homework on Interior Point Methods for Nonlinear Programming including a number of exercises.:)

Interior point methods or barrier methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems. Violation of inequality constraints are prevented by augmenting the objective function with a barrier term that causes the optimal unconstrained value to be in the feasible space.

• Interior Point Method Homework

This assignment can be completed in groups of two. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.

(:html:)

 <div id="disqus_thread"></div>
    <script type="text/javascript">
        /* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
        var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname

        /* * * DON'T EDIT BELOW THIS LINE * * */
        (function() {
            var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
            dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
            (document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
        })();
    </script>
    <noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
    <a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>

(:htmlend:)