Lecture Notes 15
Lecture 15 - Linearization
Now that we've derived nonlinear models based on material and energy balances, we need to get them into a form for linear systems analysis. We do this through a process called linearization. In Lecture 15, we review the mathematics of how to linearize a nonlinear function. We have a couple exercises to help practice the linearization process.
Linear vs. Nonlinear Models: CSTR Case Study
Linear vs. Nonlinear Models: Gravity Drained Tank Case Study
We previously ran through an example of a gravity drained tank.

Fig 1: Diagram of the Gravity Drained Tank
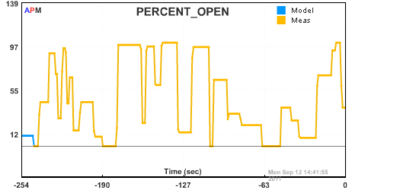
Fig 2: Sequence of Valve Movements to Test Models
We derived a FOPDT model of the process using empirical fitting techniques. A first principles approach was also used to obtain a model from a material balance. A comparison of the two models is shown below:
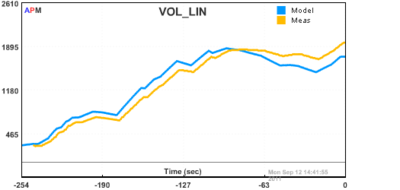
Fig 3: Linear Model (FOPDT). The linear response is easy to fit to the data but deviates, especially during the periods that are far from the steady state values.
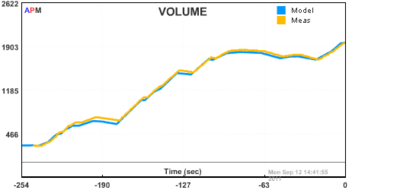
Fig 4: Nonlinear Model Based on a Material Balance. The nonlinear response is valid over a wider range of operation.
