APMonitor is designed to enable multiple modes of operation with one model. This model is defined in terms of differential and algebraic equations. The program handles all of the configuration and interfacing to the solvers. The simulation mode is changed with the APM.IMODE option.
IMODE = {1-9} % APM MATLAB example for dynamic simulation (imode=7) apm_option(server,app,'apm.imode',7); # APM Python example for model predictive control (imode=6) apm_option(server,app,'apm.imode',6) # GEKKO Python example for steady state optimization (imode=3) from gekko import GEKKO m = GEKKO() m.options.IMODE = 3
Non-linear Model Core
The core of all modes is the non-linear model. Each mode interacts with the nonlinear model to receive or provide information. There are 6 modes of operation for the APMonitor software.
- Steady-state simulation (SS)
- Model parameter update (MPU)
- Real-time optimization (RTO)
- Dynamic simulation (SIM)
- Moving horizon estimation (EST)
- Nonlinear control / dynamic optimization (CTL)
- Sequential dynamic simulation (SQS)
- Sequential dynamic estimation (SQE)
- Sequential dynamic optimization (SQO)
Modes 1-3 are steady state modes with all derivatives set equal to zero. Modes 4-6 are dynamic modes where the differential equations define how the variables change with time. Modes 7-9 are the same as 4-6 except the solution is performed with a sequential versus a simultaneous approach. Each mode for simulation, estimation, and optimization has a steady state and dynamic option.
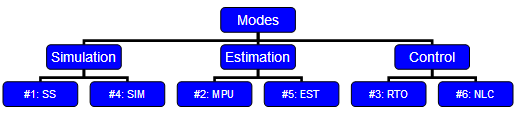
Simulation
Modes 1 and 4 are simulation-only modes. These simulation modes are for steady-state and dynamic investigation of the model. There is no optimization with the simulation modes. The model serves as a virtual process or simulator.
Estimation
Modes 2 and 5 are estimation modes. Mode 2 is for steady-state estimation and mode 5 is for dynamic estimation. Mode 2 is also known as the data reconciliation step in a real-time optimization solution. Mode 5 is also known as moving horizon estimation. Mode 5 is equivalent to the Kalman filter when the model is linear, the disturbance noise is white, and the probability density function is assumed Gaussian.
Optimization and Control
Modes 3 and 6 are optimization and control modes. Mode 3 performs steady-state optimization. Combined with mode 2, this constitutes a real-time optimization (RTO) solution. Mode 6 has a similar objective as mode 3 but is solved with a time-varying model. For linear models, this is often referred to as control. For nonlinear models, this is referred to as nonlinear control (NLC) or nonlinear model predictive control (NMPC).