Van der Pol oscillator
The Van der Pol oscillator (named for Dutch physicist Balthasar van der Pol) is a type of nonconservative oscillator with nonlinear damping. It evolves in time according to the second order differential equation:
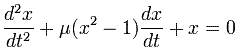
The van der Pol oscillator was originally discovered by the Dutch electrical engineer and physicist Balthasar van der Pol. Van der Pol found stable oscillations, now known as limit cycles, in electrical circuits employing vacuum tubes. When these circuits are driven near the limit cycle they become entrained, i.e. the driving signal pulls the current along with it. Van der Pol and his colleague van der Mark reported in that at certain drive frequencies an irregular noise was heard. This irregular noise was always heard near the natural entrainment frequencies. This was one of the first discovered instances of deterministic chaos.
Model
Sample Results
Input
The oscillator is driven with a sine wave forcing function at 60 Hz and amplitude 1.
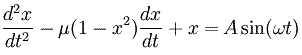
! APMonitor Modeling Language
! https://www.apmonitor.com
Model osc
Parameters
mu = 1
A = 1
omega = 2
b = 2
End Parameters
Variables
t = 0
x = b
y = b/(mu*(1-b^2))
End Variables
Equations
! time integrator
$t = 1
! oscillator
$x = y
$y + mu*(x^2-1)*$x + x = A * sin(omega*t)
End Equations
End Model